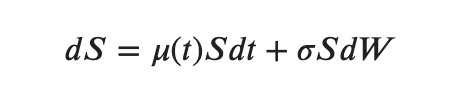
Options and the Black–Scholes Formula (Part 1)

Overview

Part 1

In this series of articles, I derive the Black–Scholes equation for valuing a European call option in the classical way.

DISCLAIMER: in these articles I’m trying to give intuition for what’s going on, so in many places I intentionally omit mathematical formalities in order not to make understanding harder.

In the previous article we discussed what options are and how they work. Now let’s derive a formula for valuing a European call option.

Don’t be afraid of all the terms as we go along — I’ll try to explain each term clearly.

Table of contents (both parts)

1. A naive view of how price moves in the market
2. Adding randomness — price movement as a random process
3. Normal and log-normal distributions
4. The price dynamics equation when the price is log-normally distributed
5. Problems with the resulting equation
6. Girsanov’s theorem and the risk-neutral measure
7. We got rid of the unknown drift. What next?

A naive view of how price moves in the market

Let’s imagine we have some risky asset that trades on an exchange. For example, the price of ether over time.

Let’s assume that we are looking for a function that gives the relative price (in fact, our S(t) is S(t)/S0).

We want to learn to make some predictions about the future price. Ideally, we would like to have some function S(t) that, at any moment in time, would tell us how much the underlying asset will cost. This can be written in differential form:

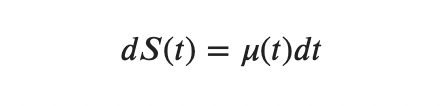
By integrating it, we get:

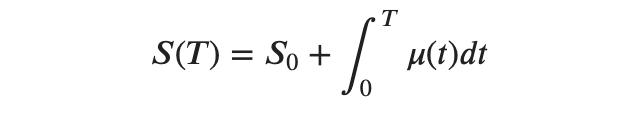
That is, a function that would tell us the future price.

Such a model has a problem.

We only see history, and nobody knows where the price of ether will go in the future. It can go up by some percentage, it can go down — in general, anything can happen. But we would like to find a function that deterministically states the future value. Because of a bunch of different reasons, it’s simply impossible to build such a deterministic function.

Adding randomness

Since we can’t say unambiguously what the price will be in the future, let’s consider a process that has two parts: a deterministic part and a stochastic part.

Normal and log-normal distributions

If we consider the process described above, then at any moment in time the value X(t) will be normally distributed (because of the σdW term, which is normally distributed).

But empirically it has been observed that in reality the distribution of the underlying price is not normal, but closer to log-normal. This is a distribution whose logarithm is normally distributed.

This can be explained by the fact that sharp crashes periodically happen in markets — some low-probability events that usually nobody takes into account (a log-normal distribution has a “long tail”).

A log-normal distribution in the real world (joke)

The price dynamics equation when the price is log-normally distributed

Initially, we wrote down a process that is normally distributed:

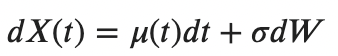
Let’s take the logarithm of the process X(t) and obtain the price dynamics equation for a price whose distribution is log-normal:

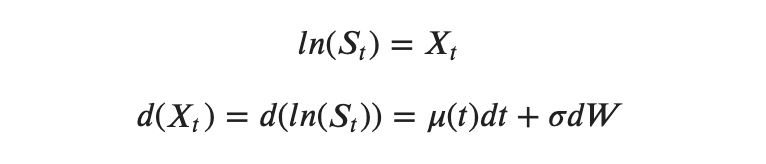
Sₜ — the price of ether at time t.

Remembering that

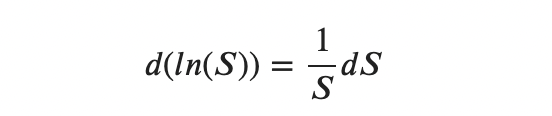
we get

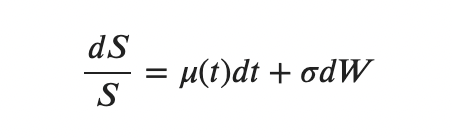
Finally, we obtain

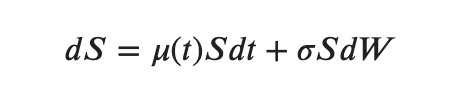
This equation is called the geometric Brownian motion equation.

We want to solve this equation, i.e., obtain a function S(T) = … (it will be non-deterministic because of the stochastic part).

Problems with the current equation

At this point there are two problems:

1. We don’t know anything about the drift μ(t). Intuitively, this is a “risk” parameter for a particular stock/coin/token (but formally the risk parameter is defined differently; later there will be a formula). And in the general case, this parameter can depend on time.
2. The resulting equation is quite hard to solve. You can’t just integrate it, because on the right-hand side there are not constants but functions μ(t)S and σS. You also can’t separate variables by moving S to the left-hand side and just integrating (a little later we’ll see why).

In the next articles, we’ll overcome these two problems.

Thanks for your time.

Stay tuned for updates.