Decomposing a Uniswap V3 Position into Two Options
Overview
In this article, I’ll show how an LP position on Uniswap v3 is related to options, and I’ll numerically compare how effective this concept is by estimating the fair values of these options and the fees earned.
I’ll also show how to estimate fair values for many derivatives, using the example of a “curved” call-spread option that appears in this article.
What this article contains
- We take a Uniswap V3 position in the “dollar — ether” pair
- We decompose the Uniswap V3 position into two options (as in the figure below)
- We estimate the fair values of the two resulting “curved” options using the SABR stochastic model calibrated to the Deribit exchange
- We backtest the Uniswap V3 position on historical data (walking block-by-block through the blockchain) to compute earned fees
- Results and analysis: we look at what the positions look like including premia and fees
- What happens if we push the upper bound of the Uniswap v3 position to infinity?
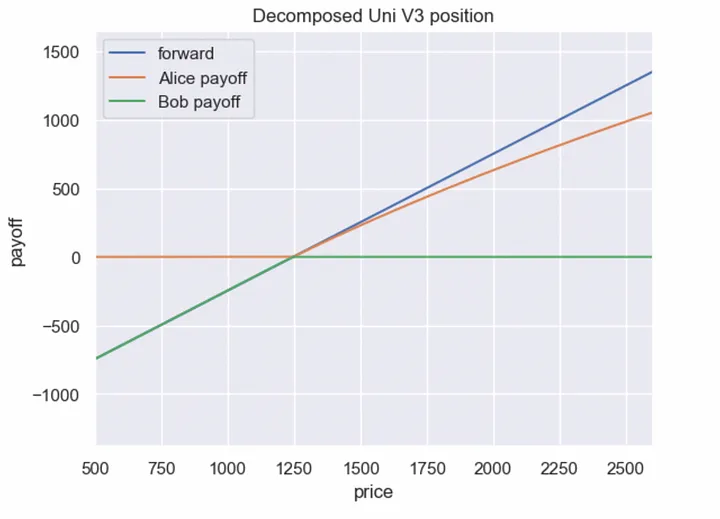
We’ll see how a Uniswap v3 position is related to two exotic options — a curved call spread and a put option (in the general case, also curved).
The option buyer receives all the positive return from the Uniswap V3 position plus the fees, while the other side effectively sells a put and receives the premium (at time t = 0).
More precisely, this is not selling a put, but selling a covered call. However, since they have the same payoff function (TV — TV₀), we’ll analyze it as selling a put.
A Position in Uniswap V3
In the following examples we consider the USDC–WETH pair (dollar — ether).
Suppose we have two users — Alice and Bob. The first user (Alice) opens a position in Uniswap V3, i.e., provides liquidity in a chosen price range.
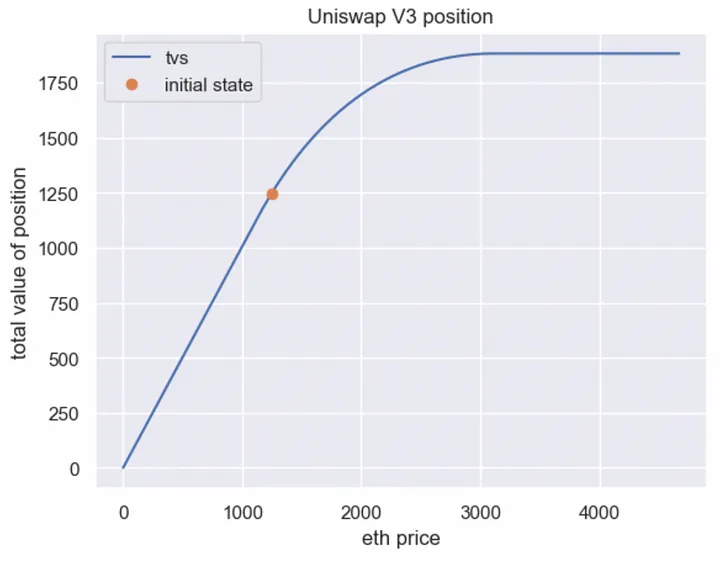
Parameters of this Uniswap position:
- Current asset price: 1247 USDC for 1 ETH
- Lower price bound: 1122 USDC (10% lower)
- Upper price bound: 3118 USDC (2.5× higher)
- Initial total value in USDC: 1247
I ran the backtest for this position roughly around January 2023.
In this position, the initial token amounts are:
- 152 USDC
- 0.87 ETH
Let’s see how the total value of this position depends on the ETH price:
Decomposing a Uniswap V3 Position
Suppose the other user (Bob) wants to buy a call option. We’ll see how Alice and Bob can make a deal that can satisfy them both.
Let’s consider the following derivative contract.
At time t = 0:
- Alice opens a Uniswap position with the specified parameters and liquidity.
- Alice locks this position for some time (i.e., she does not close it).
- Bob pays Alice a fair premium for the option he wants to buy, based on this Uniswap V3 position.
Then (after time T):
- Alice closes the Uniswap V3 position.
- If the total value of the position at that moment is greater than the initial TV, then she sends Bob the entire difference in TV. If the total value is less than the initial TV, then she keeps TV for herself.
- Alice collects all earned fees and sends them to Bob.
Let’s plot the payoff dependence on the final price at option expiry:
In the diagram above, I didn’t add option premia, since premia are needed to value such option contracts (see the next sections of this article).
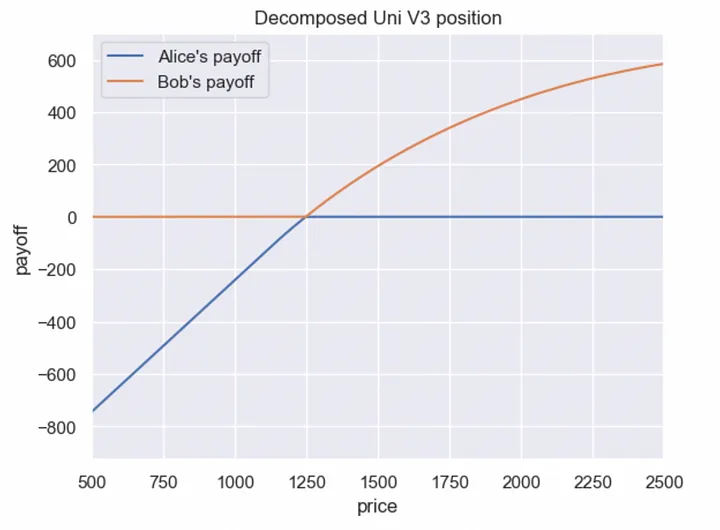
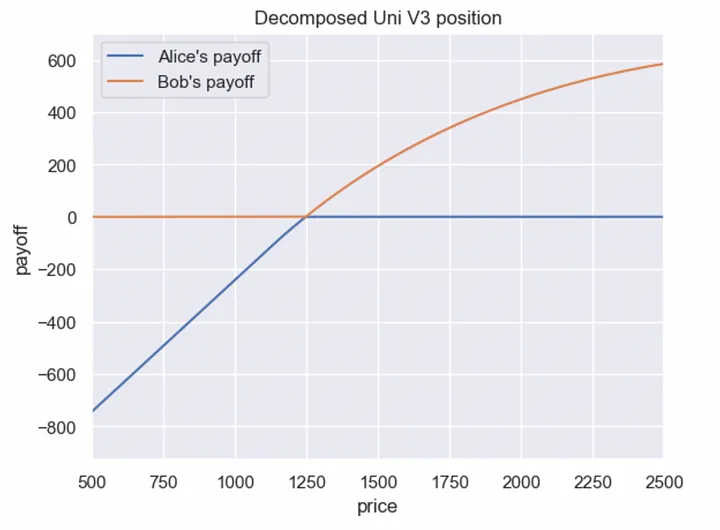
In this case, if we decompose the Uniswap V3 position, Bob gets a payoff close to a call spread — but “curved”.
At the same time, Alice’s payoff is almost exactly equal to the payoff of a sold in-the-money put option (without the option premium; we’ll add the premium after estimating the fair price of this option). For Bob, this contract is attractive because he only needs to pay a fixed premium.
Here is what the payoff graph of a “regular” call spread usually looks like:
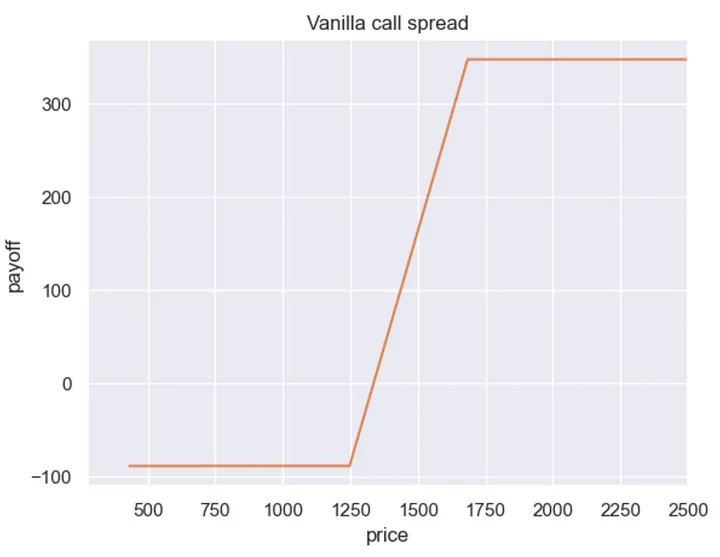
Estimating the Fair Values of the Options
Alice may be interested in selling the option to Bob if he pays a premium at least equal to the fair value of her put option.
Moreover, in this case, if Bob offers to pay more than the fair value of Alice’s put option, it will be more profitable for her to make a deal with Bob than to create a position in Uniswap V3.
Fair Price Calculation
Because of the curvature of the options under consideration, it’s impossible to use standard Black–Scholes formulas to value call and put options. In addition, the Black–Scholes model assumes constant implied volatility for all strikes, which is not realistic.
Therefore, I use a more advanced stochastic volatility model — the SABR model.
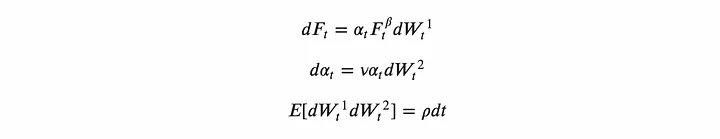
where:

This stochastic model calibrates very accurately to the volatility surface of the options market. In other words, it allows obtaining different implied volatility values depending on the chosen strike price — exactly what is needed to correctly estimate fair option values.
After calibrating the model, we can define fair prices of any exotic option contracts as the expected discounted payoff under the risk-neutral measure.
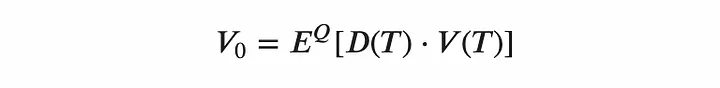

This approach is one of the core ones in traditional finance for valuing derivatives, because it implies finding the replication cost of a hedging portfolio for the chosen derivative.
I wrote in more detail about the risk-neutral measure here.
Let’s estimate the fair values of our options.
First, I calibrated the SABR model to Deribit options market data. Then, using the calibrated model, we can simulate asset price paths and obtain fair prices for any exotic option contracts using the Monte Carlo method.
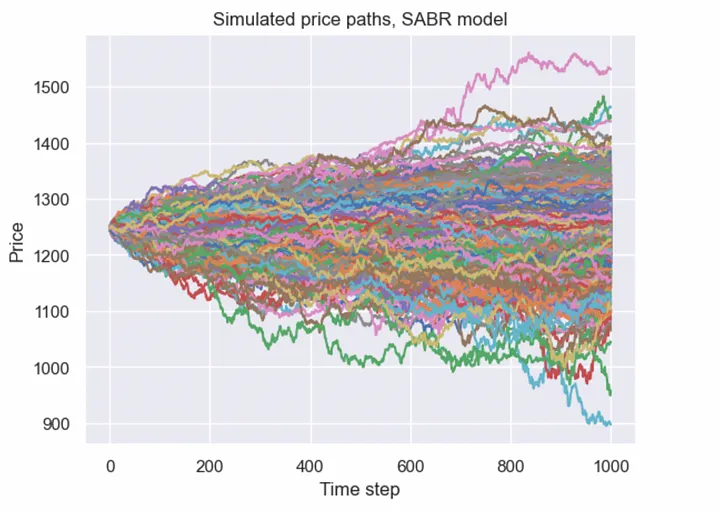
Here is an example of simulated price paths using the SABR model. It is important to note that the probability distribution is not lognormal; it is more flexible, which allows fitting the model to the market more accurately.
Fair price of this put option:
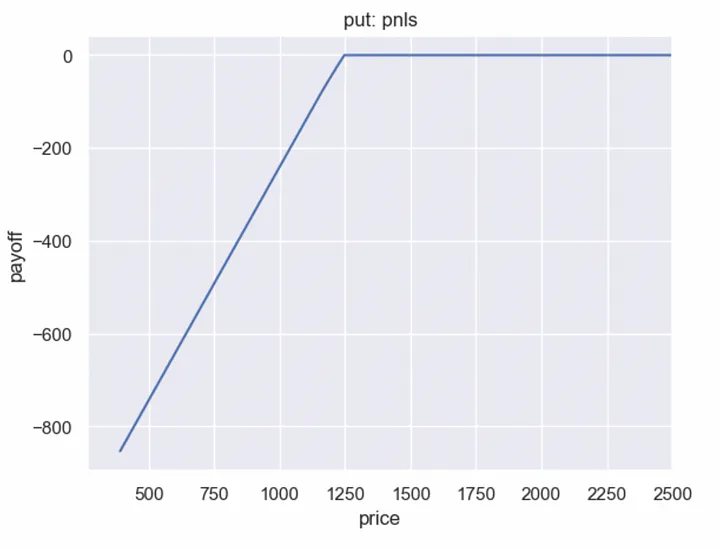
The fair price of this put option is $89.7.
Fair price of the curved call spread:
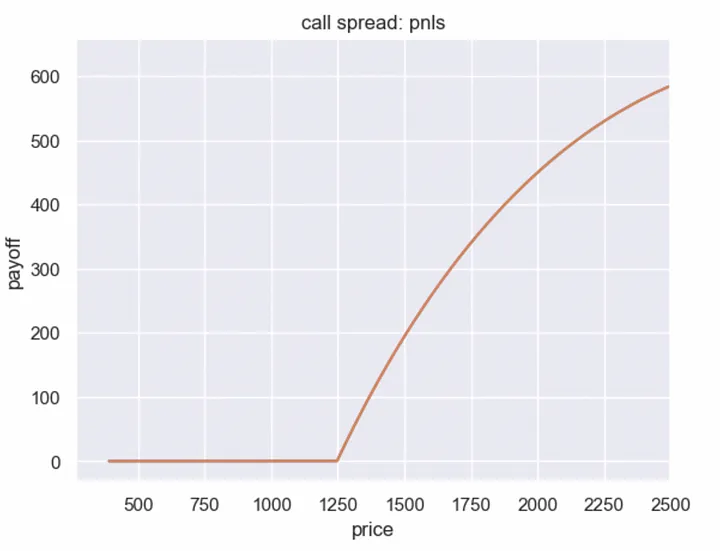
The fair price of this call spread is $70.2.
Difference between the options: 89.7 – 70.2 = $19.5.
However, our Uniswap V3 position earns fees.
How much fees will this Uniswap V3 position earn?
Let me remind you of the parameters of our Uniswap V3 position:
- Current asset price: 1247 USDC per ETH
- Lower price bound: 1122 USDC (10% lower)
- Upper price bound: 3118 USDC (2.5× higher)
- Initial total value in USDC: 1247
- Holding period: 29.2 days (time to expiration, backtest period)
Now we need to compute the expected fees earned by this position.
I backtested this LP position in Uniswap V3 on the Polygon blockchain to estimate the earned fees amount. The option pricing model was calibrated based on market option prices as of 2023-01-04 06:00:00. The backtest started from that time.
Backtest Result
The backtest of this LP position produced: earned_fees = $19.8.
This result shows that, in this case, the fair price of the put option equals the fair price of the call spread plus the earned fees. In other words, fees can compensate for the difference in option prices. Thus, both sides can potentially benefit from such a contract, since both sides get a fair price.
In addition, Bob (the option buyer) does not need to lock up any collateral; he just needs to pay the premium at time t = 0.
However, it’s worth considering that an important factor here is that the underlying price should not leave the price range of our Uniswap V3 position. And it happens quite often :-)
How Do the Positions Change Including Premia and Fees?
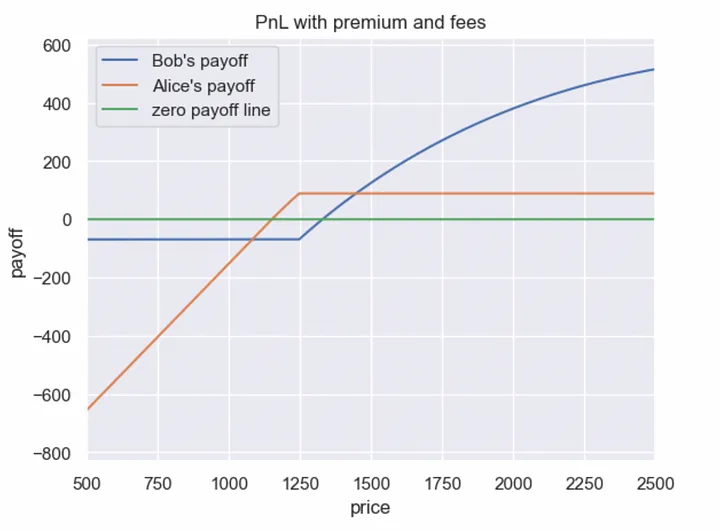
It is important to note that in this example, the fair price of the put option equals the fair price of the curved call option plus the fees generated by the Uniswap V3 position.
What happens if we move the upper price to infinity, keeping the lower price the same?
If the upper tick tends to infinity while the lower tick stays the same, then the total value of the Uniswap V3 position as a function of price becomes more linear and begins to resemble a forward contract.
As we increase the upper price, the position gets closer and closer to a standard vanilla call and vanilla put.

But we should remember that due to widening the price range, a Uniswap V3 position will generate fewer fees.
I hope I managed to show you another view of Uniswap v3 positions from the options perspective :-)